Comparing DRR and PCA

Guido Kraemer

2023-03-21

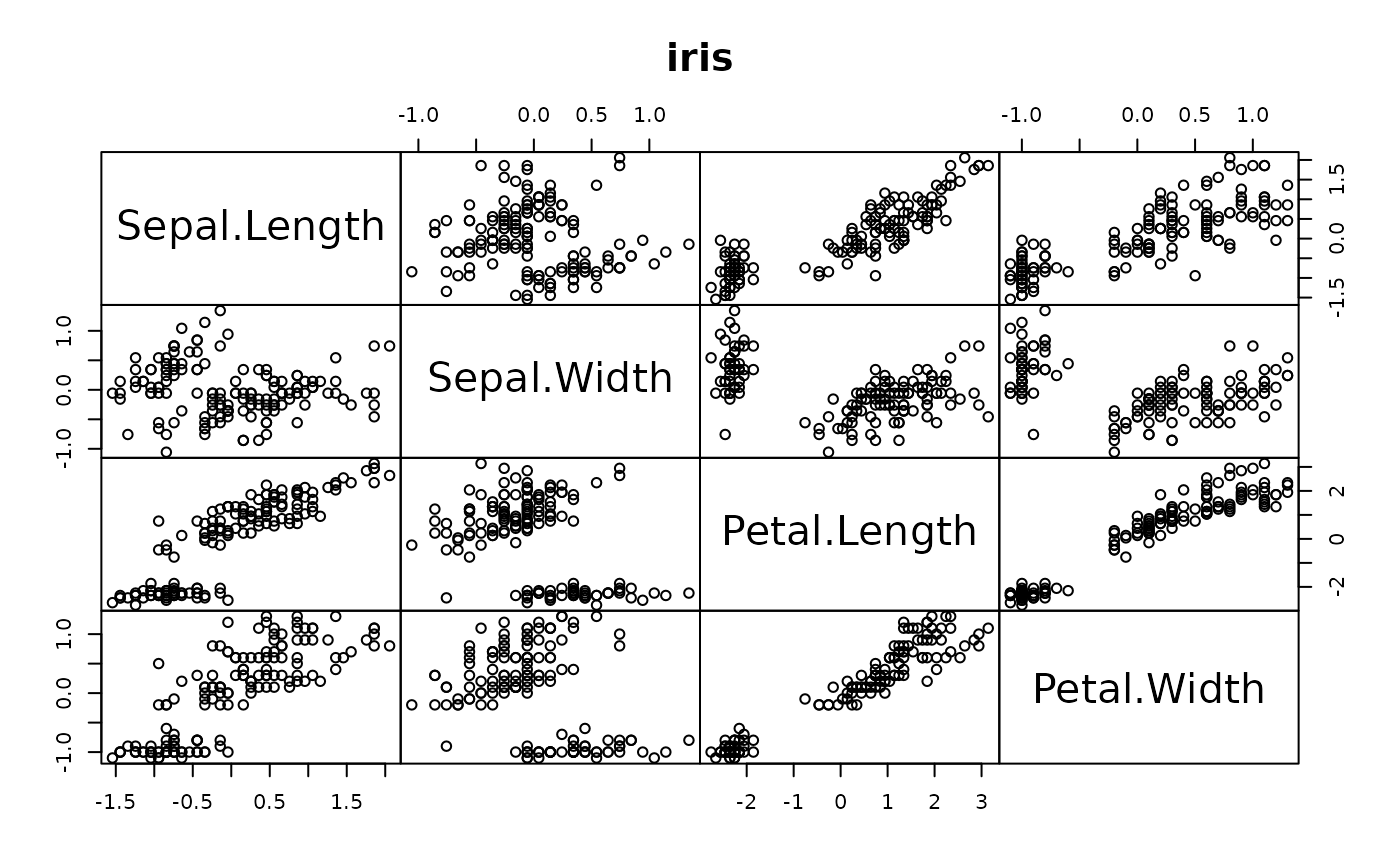
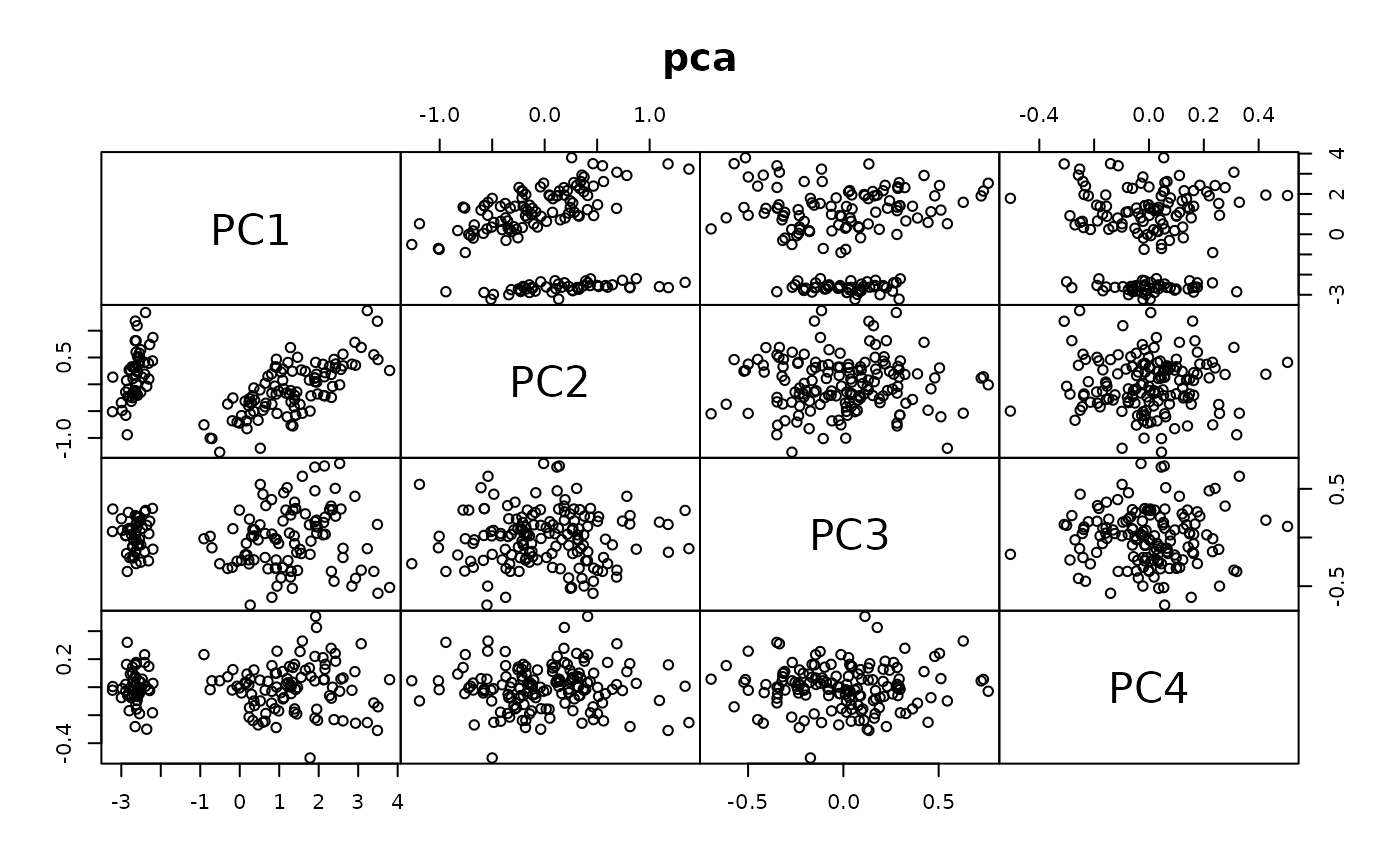
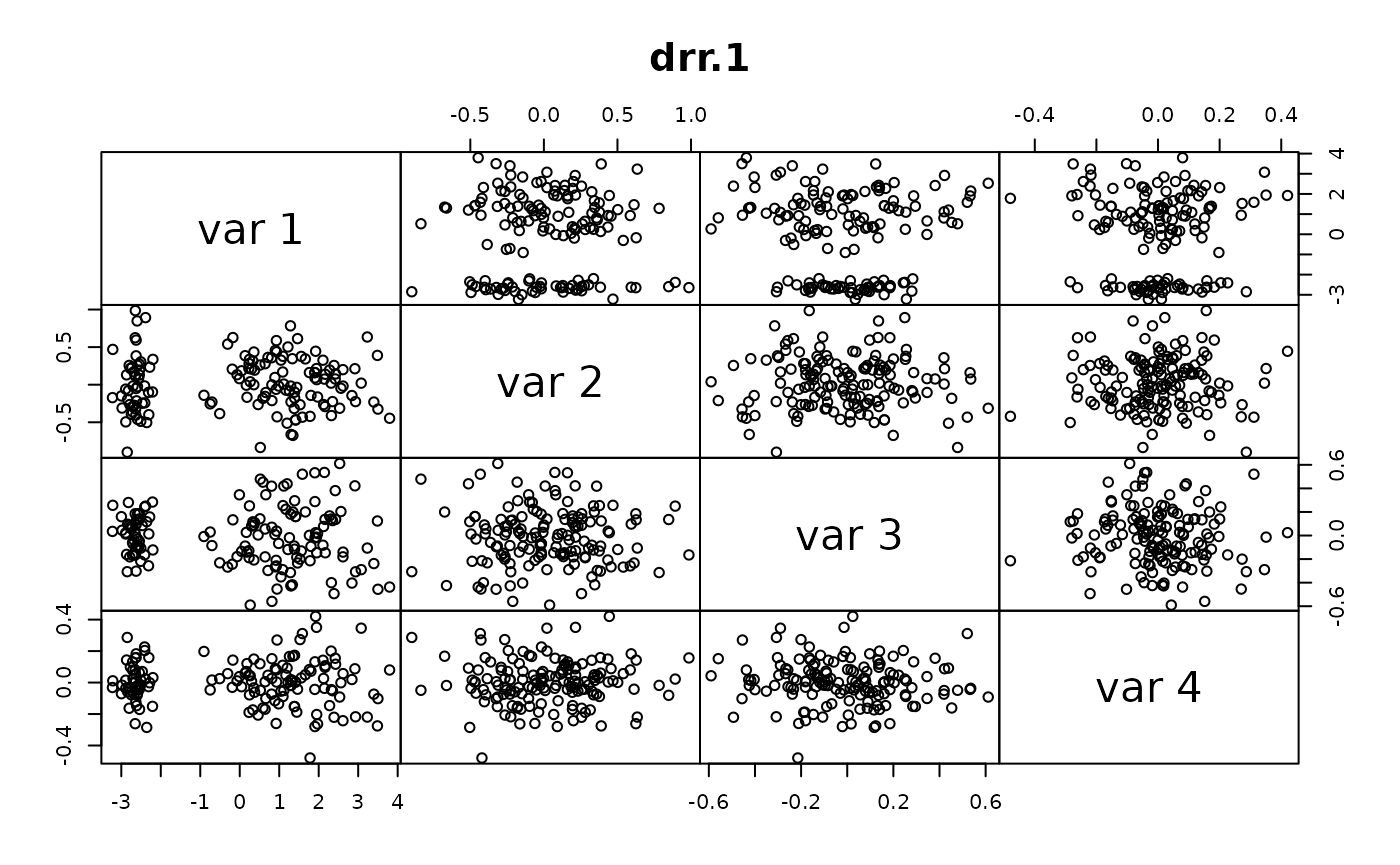
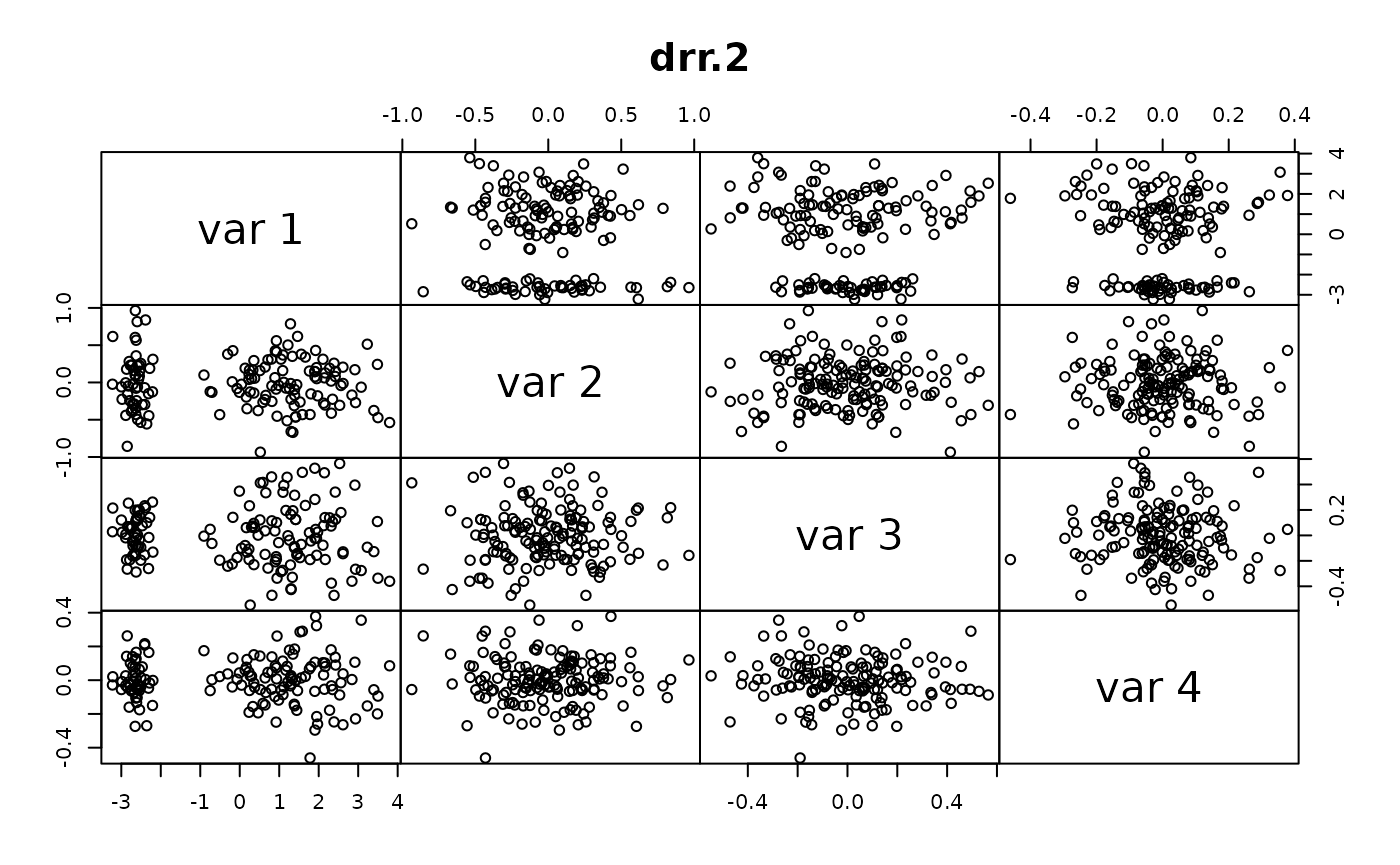
This is an example application to compare the accuracy and computational speed of DRR for different parameters to PCA.

Load libraries

library(DRR)
set.seed(123)

Read in data

data(iris)

in_data <- iris[, 1:4]

npoints <- nrow(in_data)
nvars <- ncol(in_data)
for (i in seq_len(nvars)) in_data[[i]] <- as.numeric(in_data[[i]])
my_data <- scale(in_data[sample(npoints), ], scale = FALSE)

Fit the dimensionality reductions.

t0 <- system.time(pca   <- prcomp(my_data, center = FALSE, scale. = FALSE))
t1 <- system.time(drr.1 <- drr(my_data, verbose = FALSE))
t2 <- system.time(drr.2 <- drr(my_data, fastkrr = 2, verbose = FALSE))
t3 <- system.time(drr.3 <- drr(my_data, fastkrr = 5, verbose = FALSE))
t4 <- system.time(drr.4 <- drr(my_data, fastkrr = 2, fastcv = TRUE,
                               verbose = FALSE))

Plot the data

Calculate RMSE

rmse <- matrix(NA_real_, nrow = 5, ncol = nvars,
               dimnames = list(c("pca", "drr.1", "drr.2", "drr.3", "drr.4"),
                               seq_len(nvars)))

for (i in seq_len(nvars)){
    pca_inv <-
        pca$x[, 1:i, drop = FALSE] %*%
        t(pca$rotation[, 1:i, drop = FALSE])
    rmse["pca",   i] <-
        sqrt( sum( (
            my_data - pca_inv
        ) ^ 2 ) )
    rmse["drr.1", i] <-
        sqrt( sum( (
            my_data - drr.1$inverse(drr.1$fitted.data[, 1:i, drop = FALSE])
        ) ^ 2 ) )
    rmse["drr.2", i] <-
        sqrt( sum( (
            my_data - drr.2$inverse(drr.2$fitted.data[, 1:i, drop = FALSE])
        ) ^ 2) )
    rmse["drr.3", i] <-
        sqrt( sum( (
            my_data - drr.3$inverse(drr.3$fitted.data[, 1:i, drop = FALSE])
        ) ^ 2) )
    rmse["drr.4", i] <-
        sqrt( sum( (
            my_data - drr.4$inverse(drr.4$fitted.data[, 1:i, drop = FALSE])
        ) ^ 2) )
}

The Results

More blocks for fastkrr speed up calculation, too are bad for accuracy.

RMSE

##              1        2        3            4
## pca   7.166770 3.899313 1.884524 2.059140e-14
## drr.1 5.602073 3.436881 1.709814 1.050895e-14
## drr.2 5.514719 3.211950 1.643146 1.052253e-14
## drr.3 5.726228 3.496065 1.724555 1.051144e-14
## drr.4 5.547636 2.889650 1.643971 1.089458e-14

Processing time

##       user.self sys.self elapsed
## pca       0.001    0.000   0.001
## drr.1    24.427    6.752  17.121
## drr.2    14.369    3.993   9.704
## drr.3    29.650    8.062  21.022
## drr.4    24.844    4.454  19.933